【研究】DYN和BRI

准备

Python及库若干
Vocaloid导出的文件：原始音符、DYN/BRI分别从127降到0和从0升到127的音频文件

思路

Vocaloid中每个音符的响度并不是固定的。试图通过将参数变化的音频与原始音频作差来抵消该分量。同时，元音头的重音和元音尾的渐弱也会造成一部分影响，试图通过将127~0的曲线反向，并与0~127的曲线取平均来抵消此部分影响（注：没用）。

操作

获得曲线

import matplotlib.pyplot as plt
import parselmouth as pm
import numpy as np

plt.figure(figsize=(12,6))
org=pm.Sound("E:\桌面\Original.wav").to_intensity()
trs=pm.Sound("E:\桌面\DYNfadein.wav").to_intensity()
trs2=pm.Sound("E:\桌面\DYNfadeout.wav").to_intensity()
#diff1 = 2*10**((trs.values.T- org.values.T)/20)
#diff2 = 2*10**((trs2.values.T- org.values.T)/20)
diff1 = trs.values.T- org.values.T
diff2 = trs2.values.T- org.values.T
x=np.linspace(0,127,245)
ticks=np.linspace(0,128,9)
diff = (diff1 + diff2[::-1]) /2
plt.plot(x,diff)
plt.xticks(ticks)
plt.xlabel("Value")  
plt.ylabel("dB")
plt.title("BRI Curve")
DYNdB = diff

拟合函数

from scipy.optimize import curve_fit

def funcDYNdB(x,a,k1,k2,b):
    return np.piecewise(x, [x <= a,x > a],
                        [lambda x:-k1*x**b,
                        lambda x:k2*x])
    
popt, pcov = curve_fit(funcDYNdB,x,DYNdB.squeeze(),[-30,8,8,2])
print(popt)
x=np.linspace(-64,63,245)
ticks=np.linspace(-64,64,9)
plt.plot(x,DYNdB)
plt.plot(x,funcDYNdB(x,*popt))
plt.xticks(ticks)
plt.xlabel("Value")  
plt.ylabel("dB")
plt.title("DYN Curve")

几个代码都大同小异（BRI幅度、BRI响度、DYN幅度、DYN响度），重复部分遂略。

分析

为简化分析过程，将参数为64时所对应的点设为坐标系原点。对于DYN的幅度，将DYN0对应的点设为坐标系原点。稍后会将拟合到的曲线公式编辑至博文中。

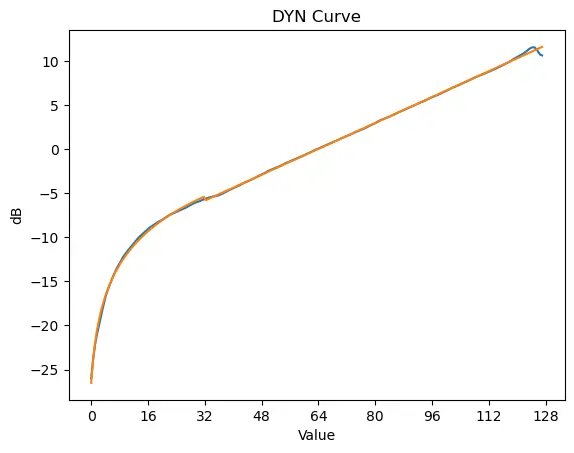
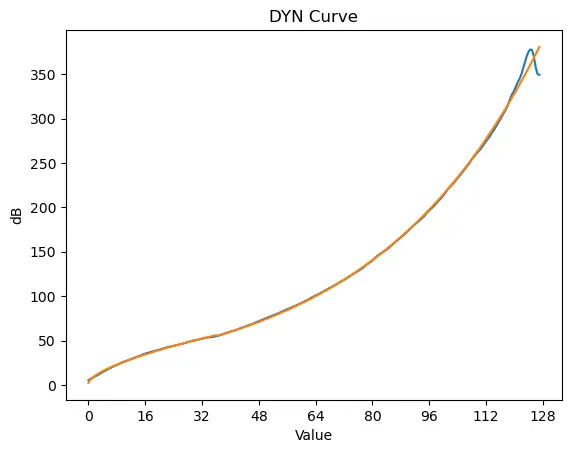
DYN

其幅度曲线具有明显的指数特性。响度曲线中，除较低参数之外则为明显的线性关系。
通过分段函数拟合后可得，DYN分段点约在36左右。DYN36以下，幅度呈线性关系，响度呈对数关系；DYN36以上，幅度呈指数关系，响度呈线性关系。
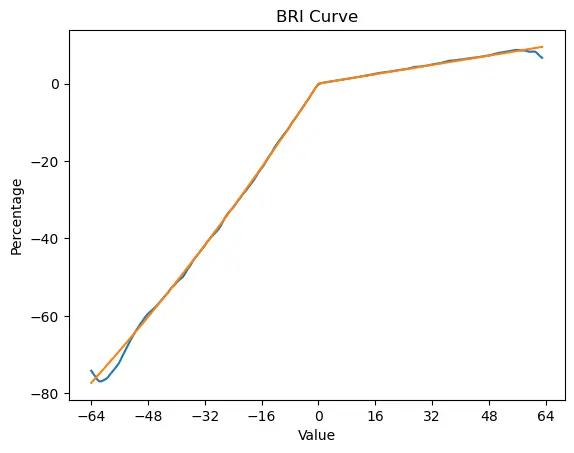
笔误：DYN-per的Y轴单位误打为dB。应为百分比%

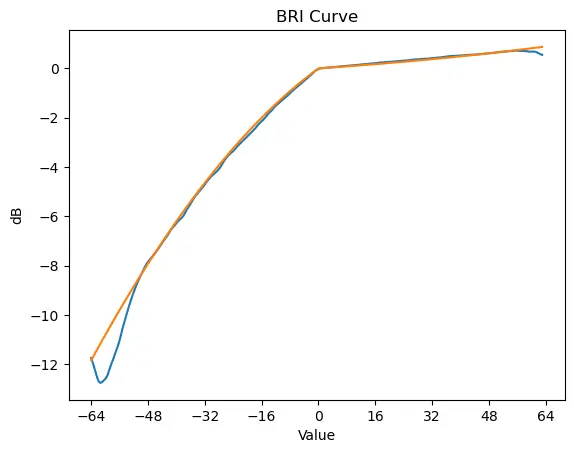
BRI

其在幅度与响度上的变化范围明显小于DYN。由于变化程度过小，导致其无论在线性域还是在对数域的函数都近似线性函数。
但其分段点明显位于64。BRI64以下，函数斜率较大，幅度和响度跟随参数的变化明显。BRI64以上，函数斜率较小，幅度和响度随参数的变化极不明显。