一些激活函数的化简
尝试通过数学公式的化简,避免一些不必要的计算,提高神经网络激活函数的计算性能。
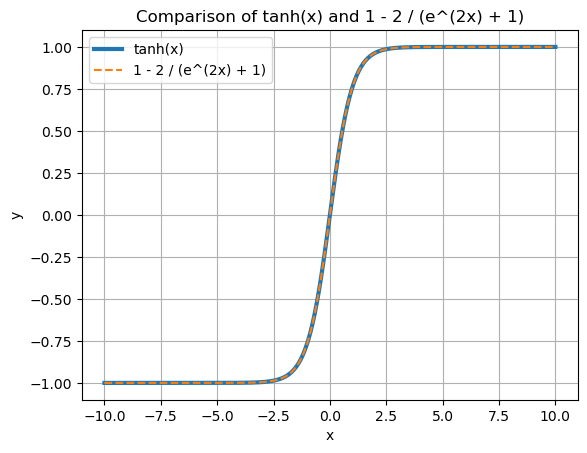
已知tanh函数:$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
在计算时需要计算两次指数函数 $e^x$ 和 $e^{-x}$ ,在计算上会比较麻烦。
通过将分式的分子分母同乘 $e^x$ ,可得:$\tanh(x) = \frac{e^{2x} - 1}{e^{2x} + 1}$
让分子通过[+1-1]来凑出分母的表达式,即:$\tanh(x) = \frac{(e^{2x} + 1) - 1 - 1}{e^{2x} + 1}$
化简得:$\tanh(x) = 1 - \frac{2}{e^{2x} + 1}$
两者对比如下:
现在将其他包含tanh函数的激活函数公式进行改写。
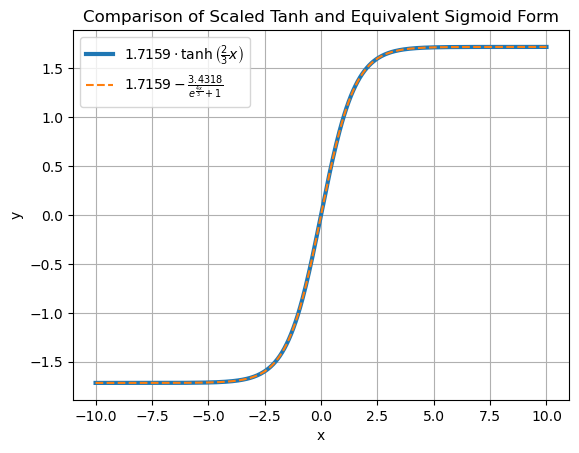
LeCun Tanh
$LeCunTanh(x) = 1.7159 \cdot \tanh\left(\frac{2}{3}x\right) = 1.7159 - \frac{3.4318}{e^{\frac{4x}{3}} + 1}$
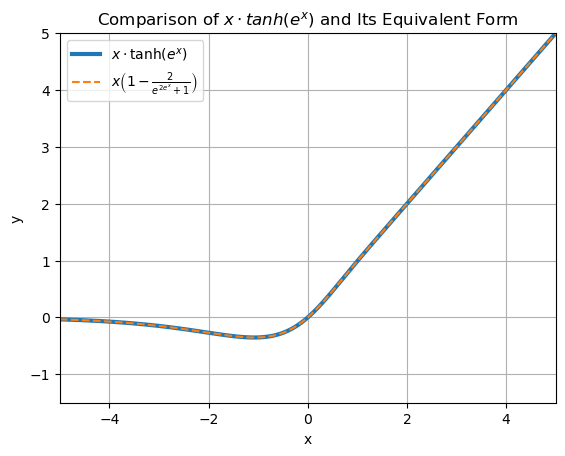
TanhExp
$TanhExp(x) = x \cdot \tanh(e^x) = x \left(1 - \frac{2}{e^{2e^x} + 1}\right)$
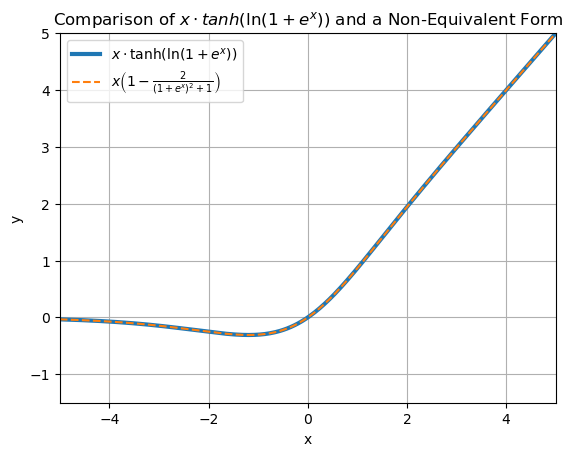
Mish
$Mish(x) = x \cdot \tanh(\ln(1 + e^x)) = x \left(1 - \frac{2}{(1+e^x)^2 + 1}\right)$
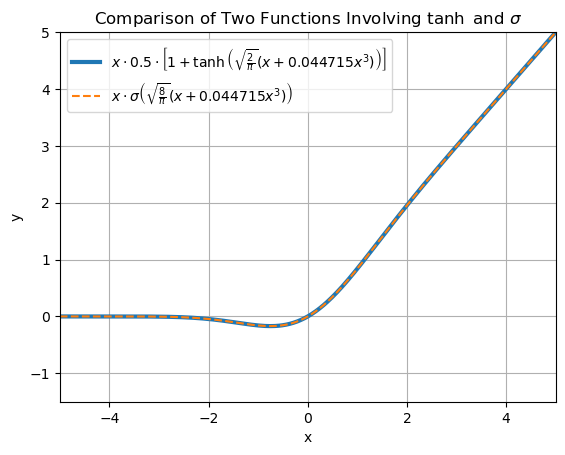
GeLU
$GeLU(x) \approx x \cdot 0.5 \cdot \left[1 + \tanh\left(\sqrt{\frac{2}{\pi}} \left(x + 0.044715 x^3\right)\right)\right] = x \cdot \left[1 - \frac{1}{e^{\sqrt{\frac{8}{\pi}} \left(x + 0.044715 x^3\right)} + 1}\right]= x \cdot \sigma\left(\sqrt{\frac{8}{\pi}} \left(x + 0.044715 x^3\right)\right)$
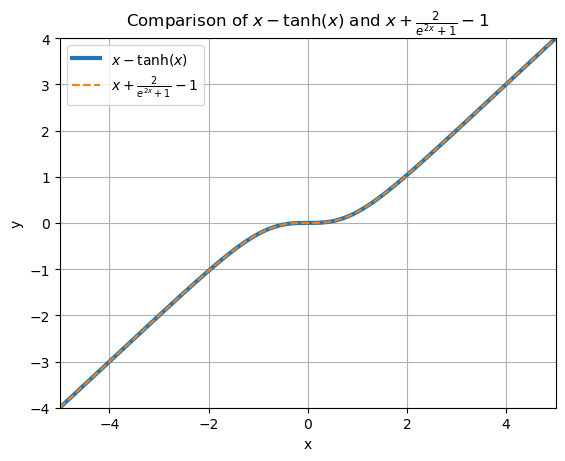
TanhShrink
$TanhShrink(x) = x - \tanh(x) = x + \frac{2}{e^{2x} + 1} - 1$